Reduced MNIST: how well can machines learn from small data?
Status: Exploratory working notes. Intended as preliminary exploration to get familiar with the problem, not as a survey of prior literature, with which I am only very incompletely familiar. Caveat emptor.
For many years, the MNIST database of handwritten digits was a staple of introductions to image recognition. Here’s a few MNIST training digits:
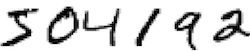
In recent years, many people have come to regard MNIST as too small and simple to be taken seriously. It has “only” 60,000 training images, each 28 by 28 grayscale pixels, and is divided into 10 classes (0, 1, 2, …, 9). By comparison, modern image recognition systems may be trained on more than a million full-color, high-resolution images, with far more classes.
For many applications it’s desirable to train using larger and more complex data sets. But from a scientific point of view it’s also extremely interesting to understand how to train machines using small, simple data sets. After all, human beings don’t need to see 60,000 examples to learn to recognize handwritten digits. Rather, we’re shown a few examples and rapidly learn to generalize. What principles underly that ability to generalize? Can machines learn to generalize from small data sets?
In these notes, I explore several simple ways of training machine learning algorithms using tiny subsets of the original MNIST data. We’ll call these subsets reduced MNIST, or RMNIST. As said in the introductory note, the notes aren’t at all complete, and I’m certainly not thoroughly familiar with prior work. Rather, this is me getting familiar with the problem by doing some basic hands-on work. Frankly, I also wanted an excuse to experiment with the scikit-learn and pytorch libraries.
The examples are based on the code in this repository.
Let’s define a few different training data sets. RMNIST/N will mean reduced MNIST with N examples for each digit class. So, for instance, RMNIST/1 has 1 training example for each digit, for a total of 10 training examples. RMNIST/5 has 5 examples of each digit. And so on. When I say MNIST, I mean the full set of images (50,000 in total, once 10,000 are held apart for validation). Here are the digits in RMNIST/1:
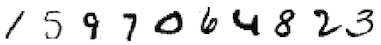
RMNIST/5:

And RMNIST/10:

These data sets are created by the program data_loader.py in the repository linked above.
Additionally, we’ll use 10,000 images from MNIST as validation data.
Baselines
To get some baseline results, we’ll use the program baseline.py. It uses the scikit-learn machine learning library, which makes it easy to implement the baselines in just a few lines of Python.
The classifiers we use include support vector machines (SVMs), with both linear and radial basis function (RBF) kernels. We also use k-nearest neighbors, decision trees, random forests, and a simple neural network. For details, see the program baseline.py. Results are shown in the table below. Classification accuracy is reported for the 10,000 validation examples.
By the way, please don’t regard this as a genuine comparison of the various techniques. I put minimal effort into configuring these, and it’s quite likely the poor performance of any given classifier is due to poor configuration or an error in my understanding, not to a defect in that type of classifier. These are baselines as a starting point for later experiments, not serious comparisons.
| Data set | SVM RBF | SVM linear | k-NN | decision tree | random forest | neural network |
|---|---|---|---|---|---|---|
| RMNIST/1 | 41.85 | 41.85 | 41.85 | 16.13 | 41.56 | 42.00 |
| RMNIST/5 | 69.73 | 69.43 | 65.08 | 34.09 | 65.70 | 69.47 |
| RMNIST/10 | 75.46 | 75.09 | 70.14 | 41.09 | 72.87 | 75.33 |
| MNIST | 97.34 | 94.81 | 97.12 | 87.51 | 88.56 | 97.01 |
Except for decision trees, all the classifiers achieved accuracies
above 40% when trained on just a single training digit from each class
(i.e., RMNIST/1). Increase the number of training examples to 5 of
each digit, and the classification performance of several classifiers
rose to near 70%. With 10 of each digit, performance rose to near
75%.
However, all these are still a long way from performance when trained on the full MNIST training data. There, several of our baselines achieved performance above 97%. Indeed, state-of-the art classifiers trained on MNIST can achieve in the neighbourhood of 99.7% or 99.8%. That’s human-level performance, since quite a few examples in the validation data are genuinely ambiguous, and there is arguably no “true” classification.
Unfortunately, I don’t know how well human beings do when trained using just very small number of example digits. As far as I know, the experiment has never been done. It would certainly be interesting to find someone who does not know arabic numerals, and see how well they could learn to classify such numerals, after being exposed to just a few examples.
With that said, I believe human beings generalize much better than our baseline classifiers. Show a small child their first giraffe and they are likely to do well at identifying later giraffes.
Can we find training strategies which let us get higher classification accuracies for RMNIST/1, RMNIST/5, and RMNIST/10?
I conjecture that it should be possible to achieve above 95% for RMNIST/1, and above 99.5% for RMNIST/10 and (perhaps) RMNIST/5, i.e., near-human performance from a small handful of training examples.
Let’s see if we can make some progress toward those goals.
Spoiler: We won’t get there. But we’ll make some progress.
Convolutional network with dropout
As a step toward better performance, let’s use a simple convolutional neural net, with dropout. The use of dropout acts as a regularizer, reducing overfitting. We can expect this to be particularly important for very small data sets. And the convolutional nature of the network reduces the number of parameters, which also helps reduce overfitting.
The convolutional network we’ll try is similar to the well-known LeNet-5 architecture. It uses two convolutional layers, with pooling, and then two fully-connected layers. For details see conv.py. We achieve classification accuracies of:
- RMNIST/1: 56.91%
- RMNIST/5: 76.65%
- RMNIST/10: 86.53%
- MNIST: 99.11%
We’re doing much better than our simple baselines! But we’re still well short of where we’d like to be.
Algorithmically expand the training data
Another idea is to algorithmically expand the training data, by doing things like making small rotations of the training images, displacing them slightly, and so on. In some sense this mirrors human learning: when a human being is shown a digit for the first time they can look at it from different angles, different distances, different positions in their field of view, and so on.
As an attempt in that direction, let’s expand the RMNIST data sets by translating them by ± 1 pixel in both the horizontal and vertical directions, and again train our convolutional network. The expansion is done by expand_rmnist.py. The resulting performance is:
- RMNIST/1: 55.25%
- RMNIST/5: 84.38%
- RMNIST/10: 92.07%
- MNIST: 99.34%
This helped significantly! In particular, we’ve exceeded 92% for RMNIST/10. That’s bad compared to modern classifiers trained on the full MNIST data set, but frankly I’m not absolutely certain a human child would do much better. However, I certainly suspect a human child would do better, and I’d very much hope we could do better with our machine classifiers.
One oddity is that performance on RMNIST/1 is not helped by expanding the training data. In fact, I did some experiments with translations of up to ± 2 pixels, and performance on RMNIST/1 was substantially improved, up to about 60%. But the results on other data sets weren’t much changed by this further expansion of the training data. It’d be good to understand this difference.
Problem: Can we get further improvement if we expand the training data by adding some jitter to the intensity of individual pixels?
Problem: Can we get further improvement if we add some small rotations to the training data?
Problem: Can we get further improvement if we expand the data using the transformations in the paper Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis, by Simard, Steinkraus, and Platt (2003)? Note, for instance, the transformations they introduce intended to mimic the natural jitter associated to vibrations of hand muscles while writing.
Problem: Are there other useful transformations one might perform to expand the training data? This is a fun-looking recent paper.
Transfer learning
So far, all our approaches to training start from the RMNIST data alone. That unfairly disadvantages the computer, since human beings don’t learn to recognize new image classes from scratch. Rather, they take advantage of what their minds already know about vision, both from experience and from evolutionary history.
We can do something similar by taking a neural network trained on some other task – something not involving MNIST – and trying to use the knowledge in that network to help us on RMNIST.
This idea is called transfer learning.
There are many approaches to transfer learning. We’ll approach it by using the pre-trained ResNet-18 network, which is built into pytorch. ResNet-18 is a deep convolutional neural network, trained on 1.28 million ImageNet training images, coming from 1000 classes. It has thus learnt an enormous amount about how to classify images in general, but not about RMNIST in particular.
We’ll take the RMNIST training and validation sets, run them through ResNet-18, and extract the high-level features in the second-last layer. The intuition is that these features contain the essential high-level information about the image, but not unimportant details. With some luck, these features will help in classifying RMNIST images.
We generate these training data sets – the high-level features for RMNIST – using the program generate_abstract_features.py. We then use transfer.py to build RMNIST classifiers based on these learnt features. The classifier we use is a fully-connected neural network with a single hidden layer containing 300 neurons. Here are the results:
- RMNIST/1: 51.01%
- RMNIST/5: 72.81%
- RMNIST/10: 82.95%
We see that transfer learning does give a considerable improvement over our baseline classifiers. However, it is well below the results we obtained earlier using our purpose-built convolutional networks.
What happens if we algorithmically expand the training data, as before, and then apply transfer learning? In that case the results get a little better, but still don’t do as well as our earlier convolutional network, even trained without the help of additional data:
- RMNIST/1: 52.84%
- RMNIST/5: 75.27%
- RMNIST/10: 84.66%
Of course, this is just one approach to transfer learning. It might be that other approaches would perform better, and it’d be worth exploring to find out. Here’s a few ideas in this vein:
Problem: Can we improve the classifier used to learn from the features derived from ResNet-18? In the experiments reported, I just used the neural net classifier built in to scikit-learn. I did some less systematic experiments using pytorch, and got to roughly 90% accuracy on RMNIST/10. It’d be good to investigate this more systematically.
Problem: What if we used networks other than ResNet-18 to do the transfer learning?
Problem: What if we used features from earlier layers in the network to do the transfer learning?
Problem: What if we used used the features learned by an unsupervised network, such as some kind of autoencoder? This has the advantage that it removes the need for labelled training data.
Problem: What if we use an ensembling approach to combine transfer learning with convolutional networks not using any kind of transfer learning?
Concluding thoughts
Our best approach to RMNIST was to use a simple convolutional net with dropout and algorithmic data expansion. That gave results of 92% on RMNIST/10, 84% on RMNIST/5, and 55% (60% with more data expansion) on RMNIST/1.
I expect it’d be easy to drive these numbers much higher just by doing more experimentation using obvious techniques. Perhaps more fun would be to explore more radical approaches to achieving high classification accuracies.
Another fun question is whether we can find super-trainers, i.e., small training sets which give rise to particularly good peformance? I chose the data for RMNIST at random from within MNIST. Might it be possible to choose subsets which result in significantly improved performance? This seems related to the problem of curriculum learning.
Even better, might it be possible to artificially synthesize very small training sets which give rise to particularly good performance? These would be true super-trainers, canonical examples from which to learn. It’d be fascinating to see what such super-trainers look like, assuming they exist.